机器学习中的求导

随机梯度下降法（SGD）是训练深度学习模型常用的优化方法，通过梯度的定义我们可以发现，梯度的求解其实就是求函数偏导的问题，导数在严格意义上说是一元的偏导
TensorFolow的自动求导就是基于返乡模式数值微分的，就是我们说的BP算法，其原理就是链式法则。实现的方式是利永反向传播与链式法则建立一张对应原计算图的梯度图，导数只是另外一张计算图，可以再次进行反向传递，对导数进行再求导以得到更高阶的导数。通过这种方式，我们仅需要一个钱箱过程和法相计算就可以计算所有参数的导数或梯度。

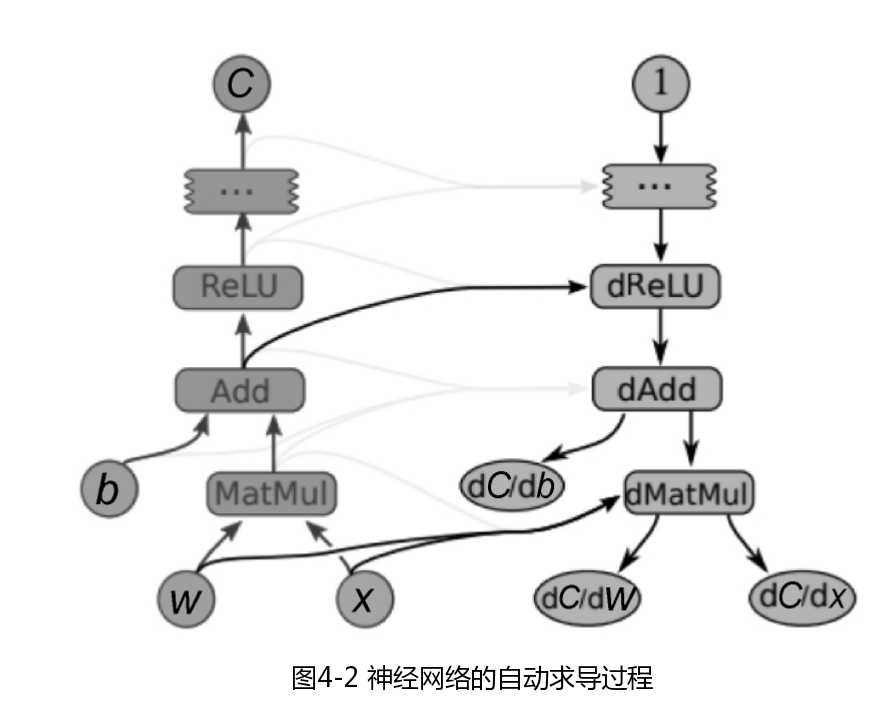
简单函数求导

在即时执行模式下，TensorFlow引入了tf.GradientTape()这个“求导记录器”来实现自动求导。

var x = tf.Variable(5.0, dtype: TF_DataType.TF_FLOAT);
            using var tape = tf.GradientTape();//在该语句后面区域的所有计算步骤都会被记录以用于求导
            var y = tf.square(x) + tf.multiply(x, 6.0f); //y=x*x+6*x
            var y_grad = tape.gradient(y, x);//计算关于X的导数y'=2*x+6

复杂函数求偏导

多元函数的偏导数以及对向量或矩阵进行求导，以下代码展示如何使用tf.GradientTape()计算函数

X=\left[\begin{array}{rr}0.5&-0.6\\0.75&1.1\end{array}\right] ,Y=\left[\begin{array}
{rr}1\\2 \end{array}\right]

在 w=(1,2)^T,b=1 时分别对w、b的偏导数

 var x = tf.constant(new[,] { { 1.0f, 2.0f }, { 3.0f, 4.0f } });
            var y = tf.constant(new[,] { { 1 }, { 2 } });
            var w = tf.Variable(new[,] { { 1.0f }, { 2.0f } });
            var b = tf.Variable(1.0f);
            using var tape = tf.GradientTape();
            var L = tf.reduce_sum(tf.square(tf.matmul(x, w) + b - y));
            var (w_grad, b_grad) = tape.gradient(L, (w, b));

---

Filed under: TensorFlow,人工智能,编程 - @ 2023年4月16日 上午11:50