线性回归
[TOC]
线性回归问题
问题描述
线性回归(Linear Regression)是回归问题中的一种,线性回归假设目标值和特征之间线性相关,即满足一个多元一次方程,通过构建损失函数,来求解损失函数最小时的参数W和b,
\hat{y}=Wx+b
式中,\hat{y}为预测值;自变量x和因变量y是已知的。我们想实现的是预测新增一个x,其对应的y是多少。因此,为了构建这个函数关系,目标是通过已知数据点,求解线性模型中W和b两个参数。
下图所示为线性函数和实际值变差示意图,其中偏离直线的点位自变量x和因变量y的实际值,这些点到直线y方向的距离线段为误差值。
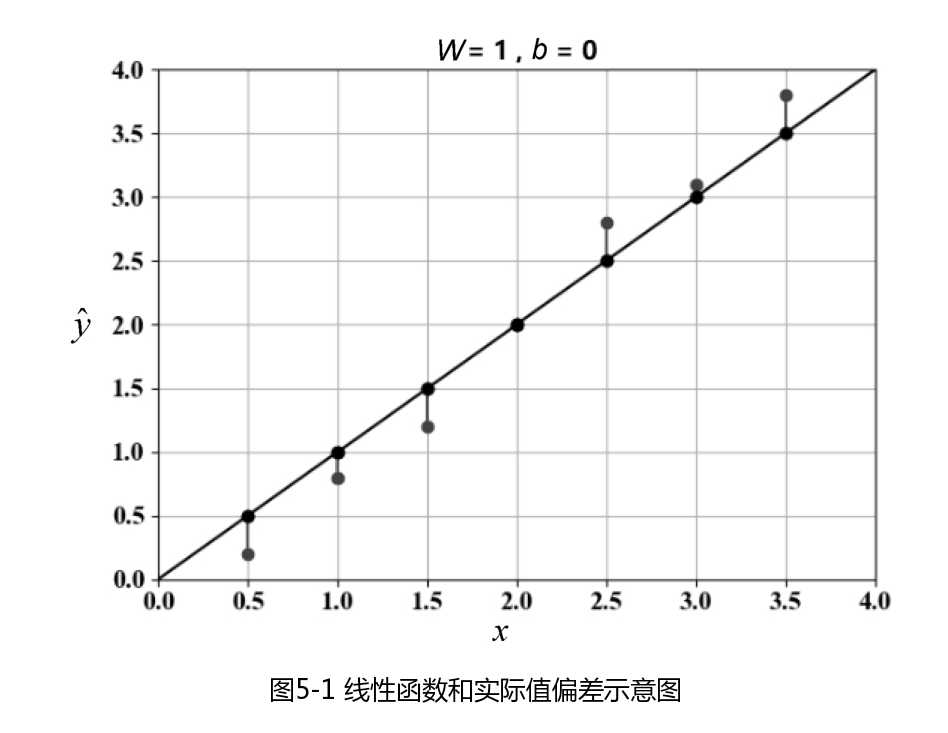
问题解析
求解最佳参数,需要一个标准来对结果进行衡量,为此我们需要定量化一个目标函数式,以便计算机在求解过程中不断地优化。
针对任何模型求解问题,最终都可以得到一组预测值\hat{y},对比已有的真实值y,数据行数n,可以将损失函数定义如下
L=\frac{1}{n}\sum_{i=1}^{n}(\hat{y}_i-y_i)^2
即预测值和真实值之间的平均的平方距离,在统计学中,一般称为均方误差(Mean square Error,MAE),把之前的函数式带入损失函数,并且将需要求解的参数W和b看做函数L的自变量,可得
L(W,b)=\frac{1}{n}\sum_{i=1}^n(Wx_i+b-y_i)^2
现在的任务是求解当L最小时,W和b的值,即核心目标优化式为
(W^*,b^*)=arg\underset{(W,b)}{min}\sum_{i=1}^n(Wx_i+b-y_i)^2
解决方案
一般采用梯度下降(Gradient Descent)法求解线性回归问题。梯度下降的核心内容是对自变量进行不断的更新(对W和b求偏导数),使得目标函数不断逼近最小值,其中,\alpha是深度学习里面的学习率。
W\leftarrow W-\alpha\frac{\partial L}{\partial W}
b\leftarrow b-\alpha\frac{\partial L}{\partial b}
使用梯度下降法,我们可以对凸问题求得全局最优解;对于非凸问题,则可以求得局部最优解
NDArray train_X = np.array(3.3f, 4.4f, 5.5f, 6.71f, 6.93f, 4.168f, 9.779f, 6.18f, 7.59f, 2.167f, 7.042f, 10.791f, 5.313f, 7.997f, 5.654f, 9.27f, 3.1f);
NDArray train_Y = np.array(1.7f, 2.76f, 2.09f, 3.19f, 1.694f, 1.573f, 3.366f, 2.596f, 2.53f, 1.221f, 2.827f, 3.465f, 1.65f, 2.904f, 2.42f, 2.94f, 1.3f);
int n_samples = (int)train_X.shape[0];
//初始化权重和偏置项
var W = tf.Variable(0f, name: "weight");
var b = tf.Variable(0f, name: "bias");
float learning_rate = 0.01f;
var optimizer = KerasApi.keras.optimizers.SGD(learning_rate);
//运行优化器进行权重和偏置项更新
int training_steps = 1000;
int display_step = 50;
foreach (var step in range(1,training_steps+1))
{
using var g = tf.GradientTape();
//线性回归模型(W*x+b)
var pred = W * train_X + b;
//MSE
var loss = tf.reduce_sum(tf.pow(pred - train_Y, 2)) / n_samples;
var gradients = g.gradient(loss, (W, b));
//应用梯度下降优化器更新W和b
optimizer.apply_gradients(zip(gradients, (W, b)));
if(step%display_step==0)
{
pred = W * train_X + b;
loss = tf.reduce_sum(tf.pow(pred - train_Y, 2)) / n_samples;
list1.Items.Add($"step:{step},loss:{loss.numpy()},W:{W.numpy()},b:{b.numpy()}");
}
}
}
Filed under: C#,TensorFlow,人工智能,编程 - @ 2023年4月16日 下午1:21