1.8 线性变换介绍
Contents
1.8 线性变换介绍
通常是把矩阵A当做一种“对象”,它通过乘法“作用”于向量x,产生的新向量称为Ax。
例如,方程:
4&-3&1&3\\
2&0&5&1\\
\end{array}\right]}_A
\underbrace{\begin{bmatrix}
1\\1\\1\\1\\
\end{bmatrix}}_x=
\underbrace{\begin{bmatrix}
5\\8
\end{bmatrix}}_b和
\underbrace{\left[\begin{array}{rrrr}
4&-3&1&3\\
2&0&5&1\\
\end{array}\right]}_A
\underbrace{
\left[\begin{array}{r}
1\\4\\-1\\3
\end{array}\right]
}_u=
\underbrace{\begin{bmatrix}
0\\
0
\end{bmatrix}}_0
乘以矩阵A后,将x变为b,将u变为零向量
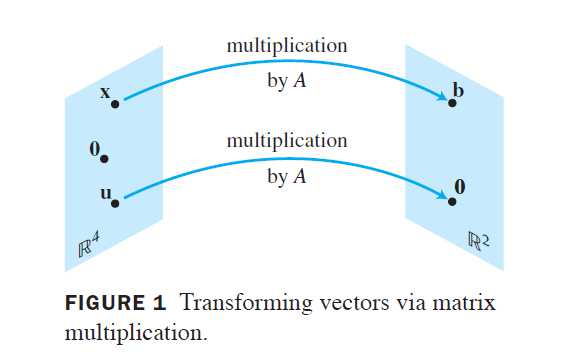
由这个新观点,解方程Ax=b就是要求出R^4中所有经过乘以A的“作用”后变为b的向量x.
由x到Ax的对应是由一个向量集到另一个向量集的函数,这个概念推广了通常的函数概念,通常的函数是把一个实数变为另一个实数的规则
由R^n到R^m的一个变换(或称函数、映射)T是一个规则,它把R^n中每个向量x对应以R^m中的一个向量T(x)。集R^n称为T的定义域,而R^m称为T的余定义域(或取值空间)。符号T:R^n\rightarrow R^m说明T的定义域是R^n而余定义域是R^m,对于R^n中向量x,R^m中向量T(x)称为x(在T作用下)的像,所有像T(x)的集合称为T的值域
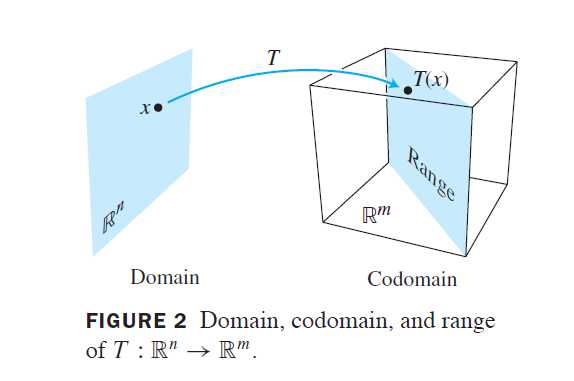
矩阵变换
对R^n中每个x,T(x)由Ax计算得到,其中A是mxn矩阵,为了简单起见,有时将这样一个矩阵变换记为x\rightarrow Ax,注意{\color{red}当A有n列时},T的定义域为R^n,而当{\color{red}A的每个列有m个元素时},T的余定义域为R^m。T的值域为A的列的所有线性组合的集合,因为每个像T(x)有Ax的形式。
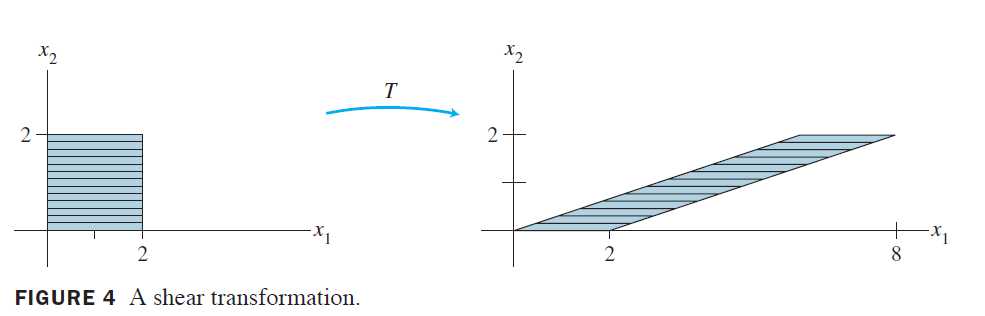
例 3 设A=\begin{bmatrix}1&3\\0&1\\\end{bmatrix},变换T:R^2 \rightarrow R^2 定义为T(x)=Ax称为剪切变换。

线性变换
若A是mxn矩阵,则变换x \mapsto Ax有以下性质:
u,v是R^n中任意向量,c是任意数。这些性质若用函数记号来表示,就得到线性代数重最重要的一类变换。
定义 变换(或映射)T称为线性的,若
1. 对T的定义域中一切 u,v,T(u+v)=T(u)+T(v)
2. 对一切u和标量c,T(cu)=cT(u)若T是线性变换,则
T(0)=0 \tag{3}且对T的定义域中一切向量u和v以及数c和d有:
T(cu+dv)=cT(u)+dT(v) \tag{4}重复应用(4)得出有用的推广:
在工程和物理中,(5)式称为叠加原理。
给定标量r,定义T:R^2 \mapsto R^2为T(x)=rx。当0 \leq r\leq1时,T称为压缩变换,当r > 1时,T称为拉伸变换。