1.9 线性变换的矩阵
Contents
从R^n到R^m的每一个线性变换,实际上都是一个矩阵变换x \mapsto Ax,而且变换T的性质都归结为A的性质。寻找矩阵A的关键,是了解T完全由它对单位矩阵I^n的各列的作用所决定。
定理 10 设T:R^n \mapsto R^m为线性变换,则存在唯一的矩阵A,使
事实上,A是mxn矩阵,它的第j列向量T(e_j),其中e_j是单位矩阵I_n的第j列:
\begin{bmatrix}
T(e_1)&\dots&T(e_n) \tag{3}
\end{bmatrix}
(3)中矩阵A称为线性变换T的标准矩阵
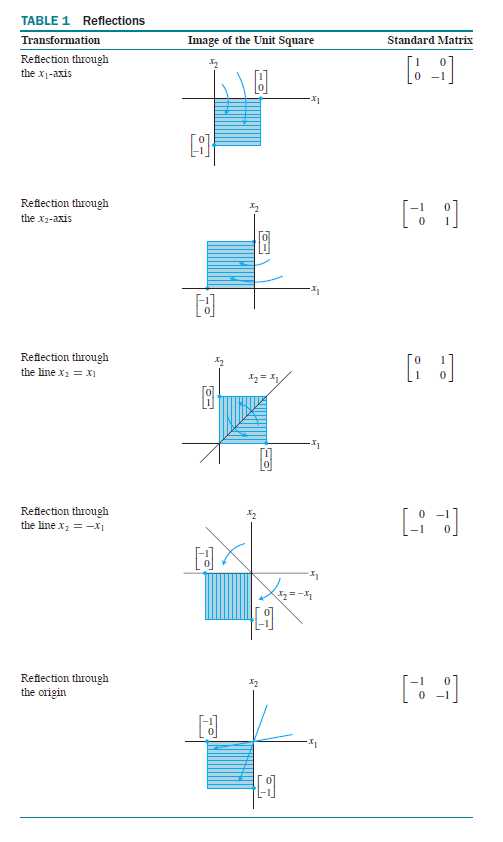
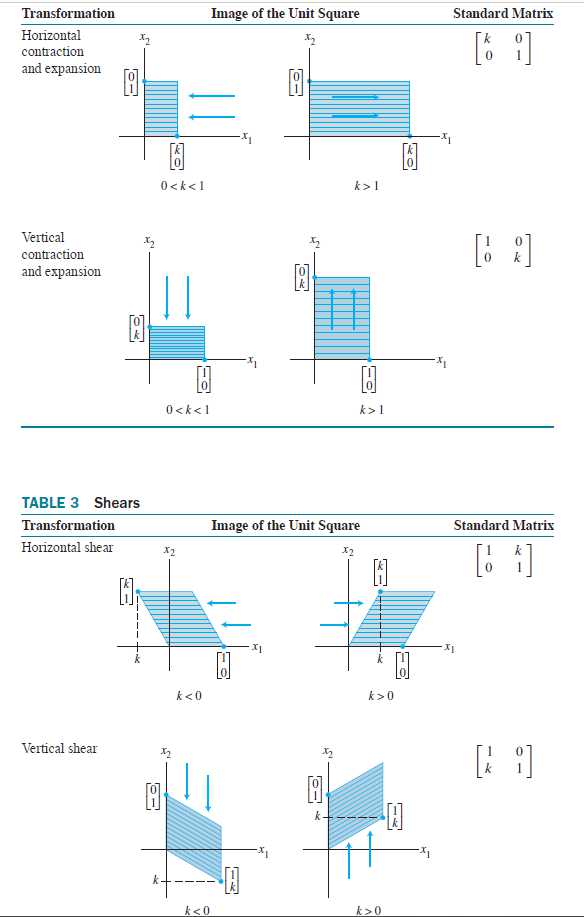
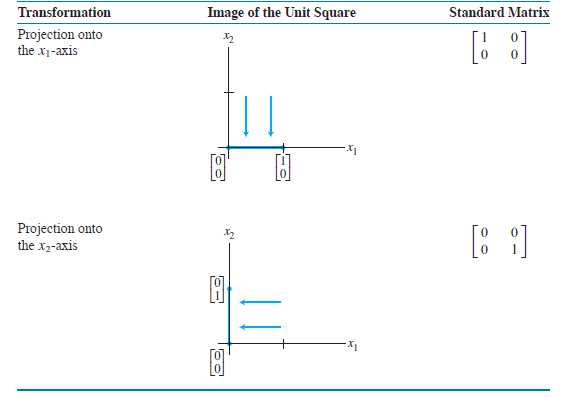
R^2中的集合线性变换
其他的变换可以通过下表列出来的变换通过复合构造出来,线性变换的复合仍是线性的。
存在与唯一性问题
线性变换的概念给出一种新的了解以前提到的存在唯一性问题的观念
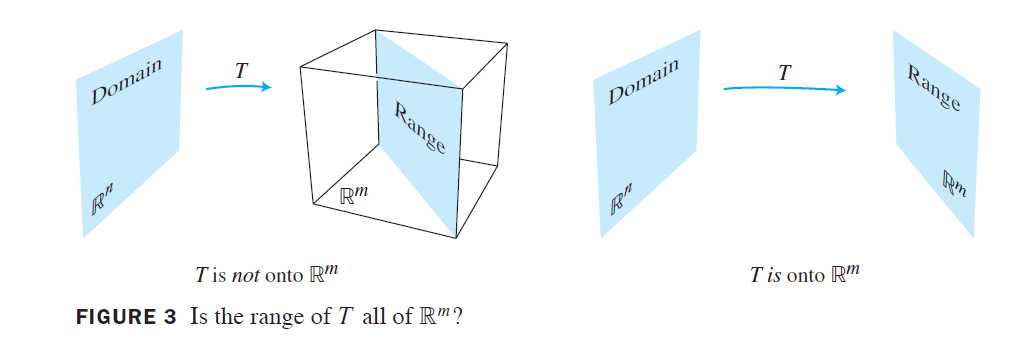
定义 映射T:R^n \mapsto R^m称为到R^m上的映射,若R^m中任一b都至少有一个R^n中的x与之对应。(也称为满射)
等价的,当T的值域是整个余定义域R^m时,T是到R^m上的。也就是说,若对R^m中没个b,方程T(x)=b至少有一个解。“T是否把R^n映射到R^m上?”是存在性问题。映射T不是到R^m上的,若R^m中有某个b使方程T(x)=b无解。
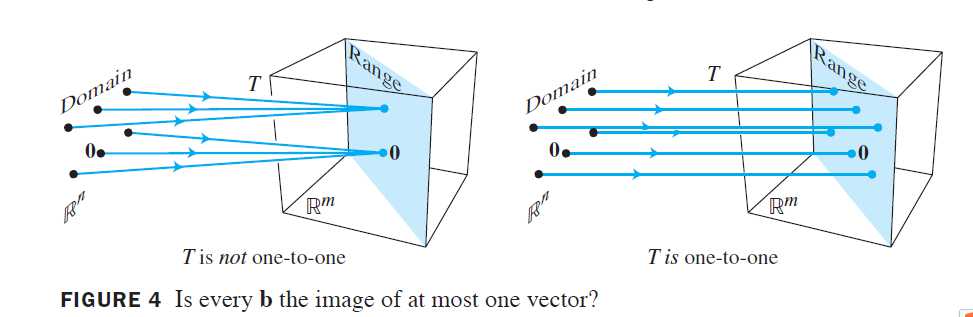
定义 映射T:R^n \mapsto R^m称为一对一映射(或1:1),若R^m中每个b是R^n中至多一个x的像(也成为单射)。
等价地,T是一对一的,若对R^m中每个b,方程T(x)=b有唯一的解或没有解。“T是否是一对一的?”是唯一性问题。映射T不是一对一的,若R^m中某个b是R^n中多个向量的像,若没有这样的b,T就是一对一的。
定理11 设T:R^n \mapsto R^m为线性变换,则T是一对一当且仅当方程Ax=0仅有平凡解
定理 12 设T:R^n \mapsto R^m是线性变换,设A为T的标准矩阵,则:
a. T把R^n映射到R^m,当且仅当A的列生成R^m
b. T是一对一的,当且仅当A的列线性无关。