第二章 矩阵代数
2.1 矩阵运算
若A是mxn矩阵,即由m行n列的矩阵,A的第i行第j列的元素用a_{ij}表示,成为A的(i,j)元素。A的各列是R^m的向量用(黑体字母)a_1,\dots,a_n表示。当我们特别注意A的各列时,我们写成A=\begin{bmatrix}a_1&a_2&\dots&a_n\end{bmatrix},注意a_{ij}是第j个列向量a_j)(从上面算起)的第i个元素。
A=\begin{bmatrix}a_{ij}\end{bmatrix}的对角元素使a_{11},a_{22},a_{33},\dots,他们组成A的主对角线。对角矩阵是一个仿真,它的非对角线元素全是0.元素全是零的mxn的矩阵称为零矩阵,用0表示,可以用0_{mxn}表示。
和与标量乘法
定理1 设A,B,C是相同维数的矩阵,r与s为数,则有
a. A+B=B+A
b. (A+B)+C=A+(B+C)
c. A+0=A
d. r(A+B)=rA+rB
e. (r+s)A=rA+sA
f. r(sA)=(rs)A
矩阵乘法
当把矩阵B乘以向量x,它将x变为向量Bx,若这向量又乘以矩阵A,结果得向量A(Bx)
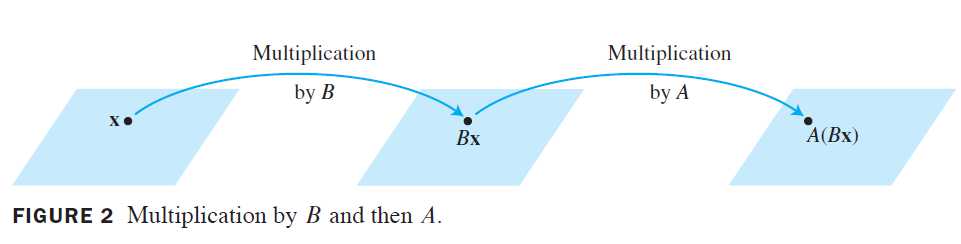
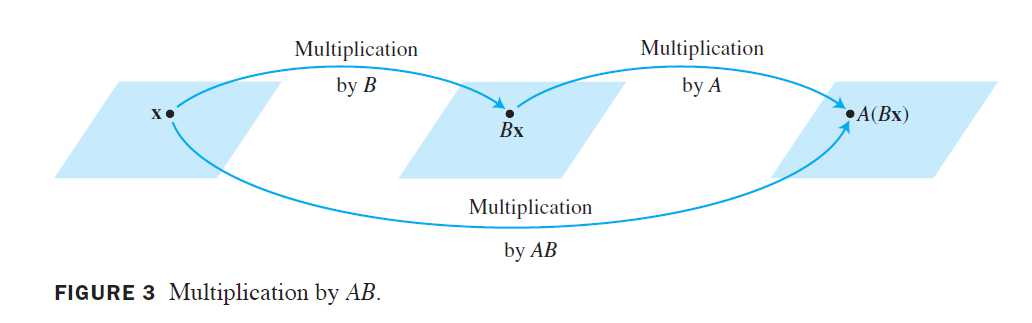
我们的目的是将此符合映射表示为乘以一个矩阵的变换,此矩阵记为AB,即
定义 若A是mxn矩阵,B是nxp矩阵,B的列是b_1,\dots,b_p,则乘积AB是mxp矩阵,它的各列是Ab_1,\dots.Ab_p,即
AB=A\begin{bmatrix}
b_1&b_2&\dots&b_p
\end{bmatrix}=
\begin{bmatrix}
Ab_1&Ab_2&\dots&Ab_p
\end{bmatrix}AB的每一列都是A的各列的线性组合,以B的对应列的元素为权。
由定义知,AB的行数等于A的行数,列数等于B的列数
计算AB的行列法则
若乘积AB有定义,AB的第i行第j列的元素是A的第i行与B的第j列对应元素乘积之和。若(AB)_{ij}表示AB的(i,j)元素,A为mxn矩阵,则
矩阵乘法的性质
I_m表示mxm单位矩阵,对R^m中的一切x,I_mx=x。
定理2 设A为mxn矩阵,B、C的维数使下列各式的乘积有定义。
a. A(BC)=(AB)C
b. A(B+C)=AB+AC
c. (B+C)A=BA+CA
d. r(AB)=(rA)B+A(rB),
e. I_mA=A=AI_n
乘积中的左右顺序是重要的,因为一般来说AB与BA并不相同。这并不奇怪,因AB的列时A的各列的线性组合,而BA的各列是B的各列的线性组合。乘积AB的银子的位置需要这样强调,即A被B右乘,或B被A左乘。若AB=BA,我们称A和B彼此可交换。
{\color{red}警告}
1. 一般情况下,AB \neq BA
2. 消去律对矩阵乘法不成立,即若AB=AC,一般情况下,B=C并不成立
3. 若乘积AB是零矩阵,一般情况下,不能断定A=0或B=0
矩阵的乘幂
若A是nxn矩阵,K是正整数,则A^k表示k个A的乘积
若A不是零矩阵,且x属于R^n,则A^kx表示x被A连续左乘k次。若k=0,则A^0x就是x本身。因此A^0被解释为单位矩阵。
矩阵的转置
给定mxn矩阵A,则A的转置是一个nxm矩阵,用A^T表示,它的列时由A的对应行构成的。
定理3 设A与B表示矩阵,其维数使下列和与积有定义,则
a. (A^T)^T=A
b. (A+B)^T=A^T+B^T
c. 对任意数r,(rA)^T=rA^T
d. (AB)^T=B^TA^T若干个矩阵的乘积的转置等于他们的转置的乘积,但相乘的顺序相反。