2.5 矩阵因式分解
Contents
矩阵A的因式分解是把A表示为两个或更多个矩阵的乘积,矩阵乘法是数据的综合(把两个或更多个线性变换的作用结合成一个矩阵),矩阵因式分解是数据的分解,在计算机科学的语言部分,将A表示为矩阵的乘积是对A中数据的预处理,把这些数据组成两个或更多部分,这种结构可能更有用,或者更便于计算。
矩阵的因式分解,以及以后的线性变换的分解将在许多关键地方出现。
LU分解
设A是mxn矩阵可以行化简为阶梯形而不必行对换(此后,我们将处理一般情形),则A可写成形式A=LU,L是mxm下三角矩阵,主对角线元素全是1,U是A的一个等价的mxn阶梯形矩阵.见下图,这样一个分解称为LU分解,矩阵L是可逆的,称为单位下三角矩阵
\begin{bmatrix}
1&0&0&0\\
\ast&1&0&0\\
\ast&\ast&1&0\\
\ast&\ast&\ast&1
\end{bmatrix}
\begin{bmatrix}
\blacksquare&\ast&\ast&\ast&\ast\\
0&\blacksquare&\ast&\ast&\ast\\
0&0&0&\blacksquare&\ast\\
0&0&0&0&0
\end{bmatrix}
在研究如何构造L和U之前,我们将看看他们为什么这么有用。当A=LU时,方程Ax=b可写成L(Ux)=b,把Ux写成y,可以由解下面一堆方程来求解x:
首先解Ly=b,然后解Ux=y求得x,没个方程都比较容易解,因为L和U都是三角矩阵。
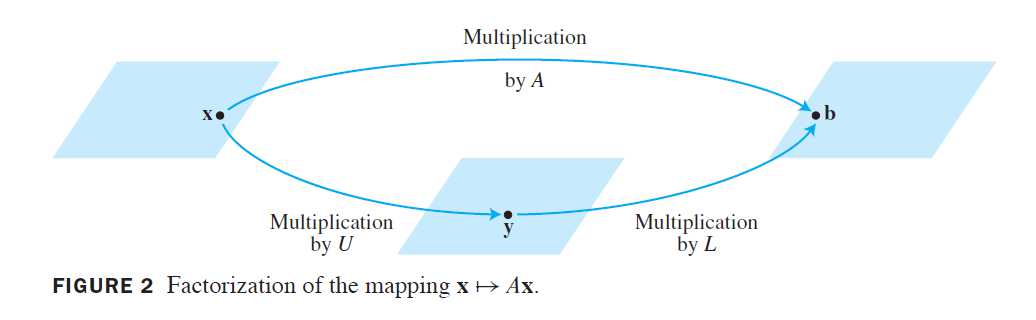
LU分解的计算效率依赖于如何求L和U
LU分解算法
设A可以化为阶梯形U。化简过程中仅用行倍加变换,即把一行的倍数加于它下面的另一行。这样,存在单位下三角初等矩阵E_1,\dots,E_p使
于是
其中
可以证明,单位下三角矩阵的逆也是单位下三角矩阵,于是L是单位下三角矩阵
注意(3)中的行变换,它把A化为U,所以也把(4)中的L化为I,因
这一点是构造L的关键。
LU分解的算法
1. 如果可能的话,用一些列的倍加变换把A化为阶梯形
2. 填充L的元素使相同的行变换把L变为I
电子工程中的矩阵因式分解
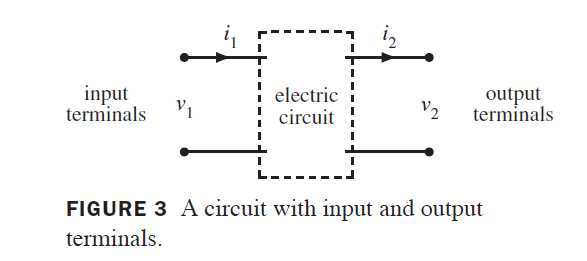
下图中的方框表示某种电路,具有输入与输出。用\begin{bmatrix}v_1\\i_1\end{bmatrix}表示输入电压与电流(电压以伏特为单位,电流用安培为单位),输入出电压与电流为\begin{bmatrix}v_2\\i_2\end{bmatrix},通常,变换\begin{bmatrix}v_1\\i_1\end{bmatrix} \mapsto \begin{bmatrix}v_2\\i_2\end{bmatrix}为线性的,也就是说,存在矩阵A,成为传递矩阵,使
v_2\\
i_2
\end{bmatrix}=
A\begin{bmatrix}
v_1\\
i_1\\
\end{bmatrix}
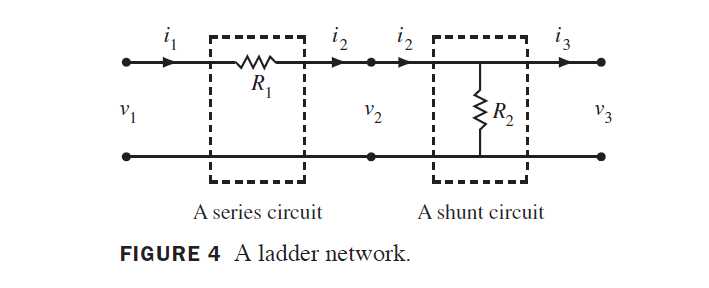
下图表示梯级网络,他有两个回路(也可以更多),他们串联起来,所以第一个电路的输出是第二个电路的输入。左边的电路称为串联电路,具有电阻R_1(单位为欧姆),有端的电路称为并联电路,有电阻R_2,应用欧姆定律,可以证明串联电路与并联电路的传递矩阵为
1&-R_1\\
0&1
\end{array}
\right]
串联电路的传递矩阵
1&0\\
-\frac{1}{R_2}&1
\end{array}
\right]
并联电路的传递矩阵