2.7 计算机图形学中的应用
屏幕上的物体的平移并不直接对应于矩阵乘法,因为平移并非线性变换。避免这一困难的标准办法是引入所谓齐次坐标。
齐次坐标
R^2中的每个点(x,y)可以对应于R^3中的(x,y,1)。他们位于xy平面上方1单位的平面上。我们称(x,y)有齐次坐标(x,y,1),例如,点(0,0)的齐次坐标为(0,0,1)。点的齐次坐标不能相加,也不能乘以数,但他们可以乘以3×3矩阵来做变换。
例 4 形如(x,y) \mapsto (x+h,y+h)的平移可以用齐次坐标写成(x,y,1) \mapsto (x+h,y+k,1),这个变换可用矩阵乘法来实现
\begin{bmatrix}
1&0&h\\
0&1&k\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\1
\end{bmatrix}=
\begin{bmatrix}
x+h\\
y+k\\
1
\end{bmatrix}
1&0&h\\
0&1&k\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\1
\end{bmatrix}=
\begin{bmatrix}
x+h\\
y+k\\
1
\end{bmatrix}
例 5 R^2中任意线性变换也可用通过齐次坐标乘以分块矩阵\begin{bmatrix}A&0\\0&1\end{bmatrix}实现,其中A是2×2矩阵,典型的例子是:
\begin{bmatrix}
cos\phi&-sin\phi&0\\
sin\phi&cos\phi&0\\
0&0&1
\end{bmatrix}
绕原点逆时针旋转角度\phi
cos\phi&-sin\phi&0\\
sin\phi&cos\phi&0\\
0&0&1
\end{bmatrix}
绕原点逆时针旋转角度\phi
\begin{bmatrix}
0&1&0\\
1&0&0\\
0&0&1
\end{bmatrix}
关于y=x的对称
0&1&0\\
1&0&0\\
0&0&1
\end{bmatrix}
关于y=x的对称
\begin{bmatrix}
s&0&0\\
0&t&0\\
0&0&1
\end{bmatrix}
x乘以s,y乘以t
s&0&0\\
0&t&0\\
0&0&1
\end{bmatrix}
x乘以s,y乘以t
复合变换
图形在计算机屏幕上的移动通常需要两个或多个基本变换,这些变换的复合相应于在使用齐次坐标时进行矩阵相乘。
齐次三维坐标
类似于二维情形,我们称(x,y,z,1)是R^3中点(x,y,z)的齐次坐标。一般地,若H \neq 0,则(X,Y,Z,H)是(x,y,z)的齐次坐标,且
x=\frac{X}{H},y=\frac{Y}{H},z=\frac{Z}{H} \tag{1}
(x,y,z,1)的每一个非零的标量乘法得到一组(x,y,z)的齐次坐标,例如(10,-6,14,2)和(-15,9,-21,-3)都是(5,-3,7)的齐次坐标。
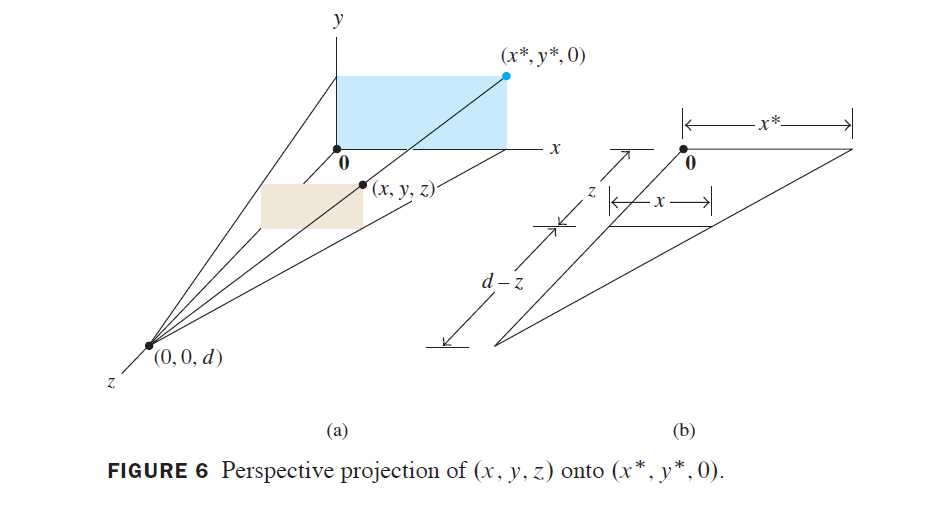
透视投影
三维物体在二维计算机屏幕上的表示方法是把它投影在一个可视平面上。(我们忽略其重要步骤,例如选择可视平面上显示在屏幕上的部分)为了简单起见,设xy平面表示计算机屏幕,假设某一观察者的眼睛向正z轴看去,眼睛的位置是(0,0,d),透视投影把没个点(x,y,z)映射为点(x^\ast,y^\ast,0),使这两点与观察者的眼睛位置(称为透视中心)在一条直线上。