矩阵的零空间

考虑下列齐次方程组

\begin{cases} x_1-3x_2-2x_3=0\\ -5x_1+9x_2+x_3=0 \tag{1} \end{cases}

用矩阵的方式，次方程组可写成Ax=0,这里

A=\left[\begin{array}{rrr} 1&-3&-2\\ -5&9&1 \tag{2} \end{array}\right]

所有满足（1）的x的集合成为方程组(1)的解集，通常将这个解集直接与矩阵 $A$ 和方程 $Ax=0$ 联系起来是方便的，我们称满足 $Ax=0$ 的所有x的集合为矩阵A的零空间。

定义　mxn矩阵A的零空间写成 $NulA$ ,是齐次方程 $Ax=0$ 的全体解的集合，用集合符号表示即
$NulA=\{x:x\in R^n,Ax=0 \}$

$NulA$ 的更进一步的描述为 $R^n$ 中在线性变换 $x \mapsto Ax$ 下映射到 $R^n$ 中零向量的庪向量的集合，见下图

定理2　mxn矩阵A的零空间是 $R^n$ 的一个子空间，等价的，m个方程、n个未知数的齐次方程组 $Ax=0$ 的全体解的集合是 $R^n$ 的一个子空间。

NulA的一个显式刻画

NulA中的向量与A中的数值之间没有明显的关系。我们称NulA被隐式地定义，这是由于它被一个必须要检验的条件所定义，没有明确地给出NulA中元素。然而，当我们解出方程Ax=0，我们就得到NulA的显式刻画。

矩阵的列空间

与矩阵相关的另一个重要的子空间是它的列空间。与零空间不同，列空间可以由向量的线性组合显式定义

定义　mxn矩阵的列空间（记为ColA）是由A的列的所有线性组合组成的集合，若 $A=\begin{bmatrix}a_1,\dots,a_n \end{bmatrix}$ ,则 $ColA=Span\{a_1,\dots,a_n\}$ 。

定理3 mxn矩阵A的列空间时 $R^m$ 的一个子空间

注意到ColA中一个典型向量可写成 $Ax$ 的形势，其中x为某向量，因为记号 $Ax$ 表示A的列向量的一个线性组合，即

ColA=\{b:b=Ax,x \in R^n\}

代表ColA中向量的记号 $Ax$ 也表明 $ColA$ 是线性变换 $x \mapsto Ax$ 的值域。

mxn矩阵A的列空间等于 $R^m$ 当且仅当方程 $Ax=b$ 对 $R^m$ 中每个b有一个解

NulA与ColA之间的对比

一个矩阵的零空间和列空间之间的关系如何是一个自然的问题，事实上，这两个空间是很不一样的。

NulA	ColA
1. $NulA$ 是 $R^n$ 的一个子空间	1. $ColA$ 是 $R^m$ 的一个子空间
2. $NulA$ 是隐式定义的，即仅给出一个 $NulA$ 中向量必须满足的条件( $Ax=0$ )	2. $ColA$ 是显式定义，即明确指出如何建立 $ColA$ 中的向量
3. 求 $NulA$ 中的向量需要时间，需要对 $\begin{bmatrix}A&0\end{bmatrix}$ 做行变换	3. 容易求出 $ColA$ 中的向量， $A$ 中的列就是 $ColA$ 中的向量，其余的可由 $A$ 的列表示出来
4. $NulA$ 与 $A$ 的数值之间没有明显的关系	4. $ColA$ 与 $A$ 的数值之间有明显的关系，因为A的列就在 $ColA$ 中
5. $NulA$ 中的一个典型向量 $v$ 具有 $Av=0$ 的性质	5. $ColA$ 中一个典型向量 $v$ 具有方程 $Ax=v$ 是相容的性质
6. 给一个特定的向量 $v$ ,容易判断 $v$ 是否在 $NulA$ 中，仅需计算 $Av$	6. 给一个特定的向量 $v$ ,弄清 $v$ 是否在 $ColA$ 中需要时间，需要对 $\begin{bmatrix}A&v\end{bmatrix}$ 作行变换
7. $NulA=\{0\}$ 当且仅当方程Ax=0仅有一个平凡解	7. $ColA=R^m$ 当且仅当方程 $Ax=b$ 对每一个 $b \in R^m$ 有一个解
8. $NulA=\{0\}$ 当且仅当线性变换 $x \mapsto Ax$ 是一对一的	8. $ColA=R^m$ 当且仅当线性变换 $x \mapsto Ax$ 将 $R^n$ 映上到 $R^m$

线性变换的核与值域

我们经常需要用线性变换而不是矩阵来表述除 $R^n$ 以外的向量空间的子空间

定义由向量空间V映射到向量空间W内的线性变换 $T$ 是一个规则,它将 $V$ 中没个向量 $x$ 映射成 $W$ 中唯一向量 $T(x)$ ，且满足：
(1)　 $T(u+v)=T(u)+T(v)$ ，对 $V$ 中所有 $u,v$ 均成立
(2)　 $T(cu)=cT(u)$ ,对 $V$ 中所有 $u$ 及所有数 $c$ 均成立

线性变换 $T$ 的核(或零空间)是 $V$ 中所有满足 $T(u)=0$ 的向量 $u$ 的集合（0为W中的零向量）， $T$ 的值域是 $W$ 中所有具有形式 $T(x)$ （任意 $x \in V$ ）的向量的集合。如果T是由一个矩阵变换得到的，比如某矩阵 $A$ ， $T(x)=Ax$ ,则 $T$ 的核与值域恰好是前面定义的 $A$ 的零空间和列空间

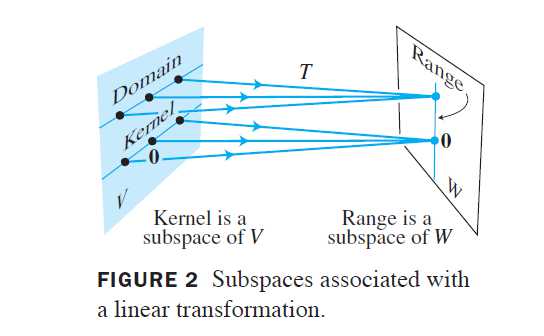
在应用中，一个子空间往往由一个适当的线性变换的核或值域产生，比如，一个齐次线性微分方程的全部解的集合被判明是一个线性变换的核。典型的，这样一个线性变换用关于一个函数的一阶或高阶导数描述

Filed under: 数学,线性代数,线性代数及其应用 - @ 2021年4月25日下午1:22

九霄之上