1.5线性方程组的解集

齐次线性方程组

线性方程组称为齐次的，若它可写成Ax=0的形式，其中A是mxn矩阵而0是R^m中的零向量，这样的方程至少有一个解，即x=0(R^n中的零向量),这个解称为它的平凡解，对给定方程Ax=0重要的是他是否有非平凡解，即满足Ax=0的非零向量x。由解的存在性与唯一性定理（定理2），得出以下事实：

齐次方程Ax=0有非平凡解，当且仅当方程至少有一个自由变量。

例2，当以方程也可看做方程组，描述下列齐次方程组的解集

10x_1-3x_2-2x_3=0 \tag{1}

解 这里无需矩阵记号，用自由变量表示基本变量x_1.通解为：
x_1=0.3x_2+0.2x_3
x_2和x_3为自由变量，写成向量形式，通解为：

x=\begin{bmatrix}
x_1\\x_2\\x_3\\
\end{bmatrix}=
\begin{bmatrix}
0.3x_2+0.2x_3\\
x_2\\
x_3\\
\end{bmatrix}=
\begin{bmatrix}
0.3x_2\\
x_2\\
0
\end{bmatrix}+
\begin{bmatrix}
0.2x_3\\
0\\
x_3\\
\end{bmatrix}\\
=x2\underbrace{\begin{bmatrix}
0.3\\
1\\
0\\
\end{bmatrix}}_u+
x3\underbrace{\begin{bmatrix}
0.2\\
0\\
1\\
\end{bmatrix}}_v(x_2,x_3为自由变量) \tag{2}

计算表明，方程（1）的每个解都是向量u和v的线性组合，如(2)式所示。即解集为Span\{u,v\}，因为，u不是v的倍数，解集是通过原点的一个平面，见下图.

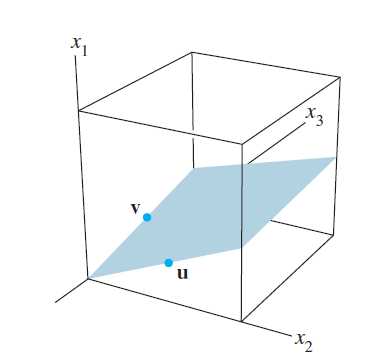
参数向量形式

最初的方程(1)是例2中的平面的隐式描述，解此方程就是要找这个平面的显式描述，就是说，将它作为u和v所生成的子集，方程(2)称为平面的参数向量方程，有时也可写为：
x=su+tv (s,t为实数)

非齐次方程组的解

当非齐次线性方程组有许多解时，一般可表示为参数的向量形式，即由一个向量加上满足对应的齐次方程的一些向量的任意线性组合的形式。
例3 描述Ax=b的解，其中

A=
\begin{bmatrix}
3&5&-4\\
-3&-2&4\\
6&1&-8\\
\end{bmatrix},b=
\begin{bmatrix}
7\\-1\\-4\\
\end{bmatrix}

解 这里A就是例1的系数矩阵。对\begin{bmatrix}A&b\end{bmatrix}作行变换得：

\left[\begin{array}{rrrr}
3&5&-4&7\\
-3&-2&4&-1\\
6&1&-8&-4\\
\end{array}\right]
\sim
\left[\begin{array}{lcr r}
1&0&-\frac{4}{3}&-1\\
0&1&0&2\\
0&0&0&0\\
\end{array}\right]
\begin{aligned}
x_1& &-\frac{4}{3}x_3=-1\\
&x_2&=2\\
& &0=0
\end{aligned}

所以x_1=-1+\frac{4}{3}x_3,x_2=2，x_3为自由变量,Ax=b的通解可写成向量形式

x=
\left[\begin{array}{r}
x_1\\
x_2\\
x_3\\
\end{array}\right]=
\left[\begin{array}{c}
-1+\frac{4}{3}x_3\\
2\\
x_3\\
\end{array}\right]
=
\left[\begin{array}{r}
-1\\
2\\
0\\
\end{array}\right]+

\left[\begin{array}{c}
\frac{4}{3}x_3\\
0\\
x_3\\
\end{array}\right]\\=
\underbrace{
\left[\begin{array}{r}
-1\\
2\\
0\\
\end{array}\right]}_p
+x_3
\underbrace{
\left[\begin{array}{c}
\frac{4}{3}\\0\\1
\end{array}\right]
}_v

方程x=p+x_3v，或用t表示一般参数，

x=p+tv (t为实数) \tag{3}

就是用参数向量形式表示Ax=b的解集。回忆例1中Ax=0的解集有参数向量形式

x=tv \tag{4}

(v与（3）中的v相同)，故Ax=b的解可由向量p加上Ax=0的解得到，向量p本身也是Ax=b的一个特解(在(3)中对应t=0)。
称（3）为通过p平行于v的直线方程。于是Ax=b的解集是一条通过p而平行于Ax=0的直线

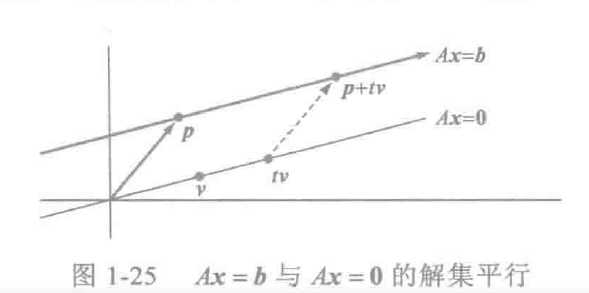
定理6 设方程Ax=b对某个b是相容的，p为一个特解，则Ax=b的解集是所有形如w=p+v_h的向量的集，其中，v_h是齐次方程Ax=0的任意一个解.
定理6说明若Ax=b有解，则解集可由Ax=0的解平移向量p得到，p是Ax=b的任意一个特解。

把相容方程组的解集表示成参数向量形式

Filed under: 数学,线性代数,线性代数及其应用 - @ 2021年4月30日 上午6:48