1.3 向量方程
线性方程组的重要性质都可以用向量概念与符号来描述。
R^2 中的向量
仅含有一列的矩阵称为列向量,或简称向量:
\begin{bmatrix}
3\\
-1
\end{bmatrix}
,v=
\begin{bmatrix}
0.2\\
0.3\\
\end{bmatrix},
w=
\begin{bmatrix}
w_1\\
w_2\\
\end{bmatrix}
这里w_1,w_2是任意实数,所有两个元素的向量的集记为R^2,R表示向量中的元素是实数,而指数2表示每个向量包含两个元素。
有时为了方便,我们把列向量
写成(3,-1)的形式,这时候,用圆括弧表示向量,并在两个元素之间加上逗号,以区别1×2行矩阵
3&-1
\end{bmatrix}
于是:
3\\-1
\end{bmatrix}\neq
\begin{bmatrix}
3&-1
\end{bmatrix}
因为这两个矩阵的维度不同,尽管他们有相同的元素
R^2 的几何表示
考虑平面上的直角坐标系。因平面上每个点由实数的有序对确定,我们可把几何点(a,b)与列向量 \begin{bmatrix}a\\b\end{bmatrix} 等同,所以可以把R^2看做平面上所有点的集合。
R^n 中的向量
若n是正整数,R^n表示所有n个实数数列(或有序n元组)的集合,通常写成nx1列矩阵的形式,如:
u_1\\
u_2\\
\vdots\\
u_n
\end{bmatrix}
所有元素都是零的向量称为零向量,用0表示(0中元素的个数可由上下文确定)
R^n中向量的代数性质
对R^n中的一切向量u,v,w以及标量c和d
1. u+v=v+u
2. (u+v)+w=u+(v+w)
3. u+0=0+u=u
4. u+(-u)=-u+u=0
5. c(u+v)=cu+cv
6. (c+d)u=cu+du
7. 1u=u
其中-u表示(-1)u
线性组合
给定R^n中向量v_1,v_2,\cdots,v_p和标量c_1,c_2,\cdots,c_p,向量
y=c_1v_1+\cdots+c_pv_p
称为向量v_1,v_2,\cdots,v_p以c_1,c_2,\cdots,c_p为权的线性组合
向量方程
x_1a_1+x_2a_2+\cdots+x_na_n=b
和增广矩阵为\begin{bmatrix}
a_1&a_2&\cdots&a_n&b \tag{5}
\end{bmatrix}的线性方程组有相同的解集。特别地,b可以表示为a_1,a_2,\cdots,a_n的线性组合,当且仅当对应于(5)式的方程组有解。
线性代数的一个主要思想是研究可以表示为某一固定向量集合
的线性组合的所有向量
定义 若v_1,v_2,\dots,v_p是R^n中的向量,则v_1,v_2,\dots,v_p的所有线性组合所成的集合用记号
Span\{v_1,v_2,\dots,v_p\}表示,称为由v_1,v_2,\dots,v_n所生成(或张成)的R^n的子集,也就是说,
Span\{v_1,v_2,\dots,v_p\}是形如:
c_1v_1+c_2v_2+\dots+c_nv_n的向量的集合,其中c_1,c_2,\dots,c_p为标量
要判断向量b是否属于
,就是判断向量方程x_1v_1+x_2v_2+\dots+x_pv_p=b是否有解,或等价地,判断增广矩阵为\begin{bmatrix}v_1&v_2&\dots&v_p&b\end{bmatrix}的线性方程组是否有解。
注意Span\{v_1,v_2,\dots,v_p\}包含v_1的所有倍数,因cv_1=cv_1+0v_2+\dots+0v_p,特别地,它一定包含零向量。
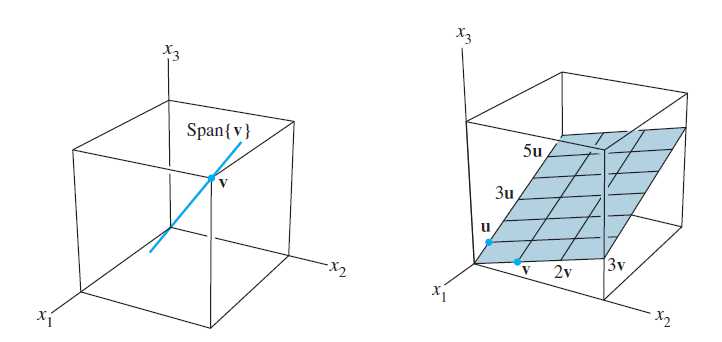
Span\{v\}与Span\{u,v\}的集合解释
设v是R^3中的向量,那么Span\{v\}就是v的所有数量倍数的集合,也就是通过v和0的直线上的所有点的集合,
若u和v是R^3中的非零向量,v不是u的倍数,则Span\{u,v\}是R^3中通过u,v和0的平面,特别地,Span\{u,v\}包含R^3中通过u与0的直线,也包含通过v与0的直线