4.4 坐标系
对一个向量空间V,明确指定一个基\beta的一个重要原因是在V上强加一个“坐标系”。本节我们将证明如果\beta包含n个向量,则坐标系将使V像R^n一样便于操作。若V就是R^n本身,则\beta将确定一个坐标系,它给V以一个新的“视野”
定理7 (唯一标示定理)
令\beta=\{b_1,\dots,b_n\}是向量空间V的一个基,则对V中每个向量x,存在唯一的一组数c_1,\dots,c_n使得x=c_1b_1+\dots+c_nb_n \tag{1}定义 假设集合\beta=\{b_1,\dots,b_n\}是V的一个基,x在V中,x相对于基\beta的坐标(或x的\beta-坐标)是使得x=c_1b_1+\dots+c_nb_n的权c_1,\dots,c_n。
若c_1,\dots,c_n是x的\beta-坐标,则R^n中的向量\begin{bmatrix}
x
\end{bmatrix}_{\beta} =
\left[\begin{array}{}
c_1\\
\vdots\\
c_n
\end{array}\right]是x(相对于\beta)的坐标向量,或x的\beta-坐标向量,映射x \mapsto \begin{bmatrix}x\end{bmatrix}_{\beta}称为(由\beta确定的)坐标映射。
坐标的几何意义
一个集合上的坐标系由此集合中点到R^n中的一一映射组成。例如,当我们选取垂直的轴同时在每个轴上取一个相同的度量单位时,通常的图纸给出了平面上的一个坐标系。
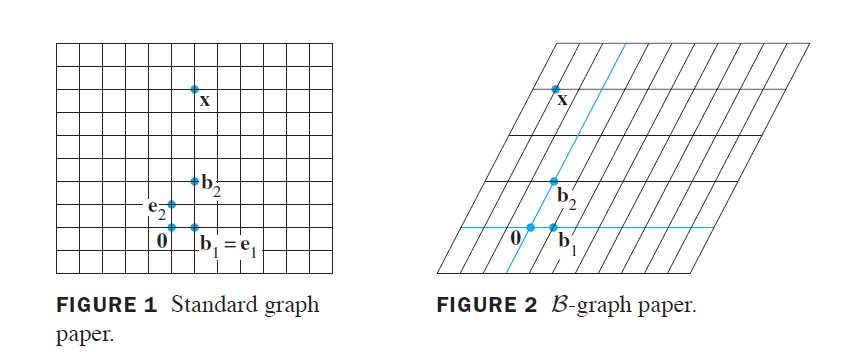
R^n中的坐标
当R^n中的一组基\beta固定时,容易求出任一指定的向量x的\beta-坐标。
2&-1\\
1&1\\
\end{array}\right]
\left[\begin{array}{rr}
c_1\\
c_2\\
\end{array}\right]=
\left[\begin{array}{rr}
4\\
5\\
\end{array}\right] \tag{3}
(3)式中的矩阵将向量x的\beta-坐标变为x的标准坐标。对R^n中的一个基\beta=\{b_1,\dots,b_n\},可以实施类似的坐标变换。令
则向量方程
等价于
我们称P_\beta为从\beta到R^n中标准基的坐标变换矩阵。通过左乘P_\beta将坐标向量$\begin{bmatrix}x\end{bmatrix}\beta变换到x.坐标变换方程(4)是重要的。
由于P\beta的列构成R^n的一个基,P_\beta是可逆的(由可逆矩阵定理),通过左乘P^{-1}_{\beta}又将x变回\beta-$坐标向量:
这里又$P^{-1}{\beta}产生的映射x \mapsto \begin{bmatrix}x\end{bmatrix}\beta是前面提到的坐标映射。因为P^{-1}_\beta是一可逆矩阵,由可逆矩阵定理(也可以参见1.9节定理12),此坐标映射是一个由R^n到R^n$上的一一线性变换。
坐标映射
对向量空间V选定一个基\beta=\{b_1,\dots,b_n\},它引出V中一个坐标系。坐标映射x \mapsto \begin{bmatrix}x\end{bmatrix}_\beta将可能不熟悉的空间V与熟悉的空间R^n联系了起来。见下图,V中的点现在可以由他们的新“名字”来确定。
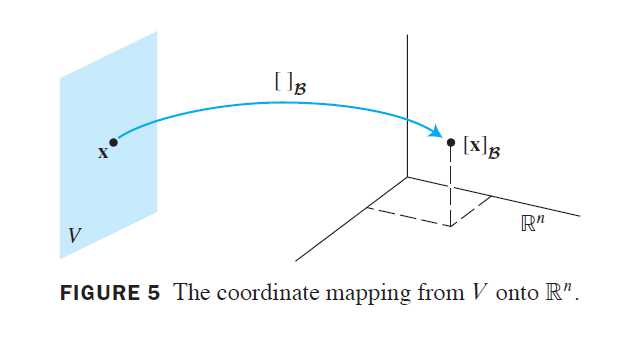
定理8 令\beta=\{b_1,\dots,b_n\}是向量空间V的一个基,则坐标映射x \mapsto \begin{bmatrix}x\end{bmatrix}_\beta是一个由V映上到R^n的一对一的线性变换。
定理8中的坐标映射是一个由V到R^n上同构的重要例子。一般而言,从一个向量空间V映上到另一个向量空间W的一一线性变换称为从V到W上的一个同构。每一个在V中的向量空间的计算可以完全相同地出现在W中,反之亦然。
