4.7 基的变换
对一个n维向量空间V,当一个基\beta取定之后,与之相关的映射到R^n上的坐标映射对V提供了一个坐标系。V中每个向量x由它的\beta-坐标向量\begin{bmatrix}x\end{bmatrix}_\beta唯一确定。
定理15设\beta=\{c_1,\dots,c_n\}是向量空间V的基,则存在一个nxn矩阵\underset{C \leftarrow\beta}{P}使得
\begin{bmatrix}x\end{bmatrix}_C=\underset{C \leftarrow \beta}{P}\begin{bmatrix}x\end{bmatrix}_\beta \tag{4}\underset{C \leftarrow \beta}{P}的列时基\beta中向量的C-坐标向量,即
\underset{C \leftarrow \beta}{P}=\begin{bmatrix}\begin{bmatrix}b_1\end{bmatrix}_C&\begin{bmatrix}b_2\end{bmatrix}_C&\dots&\begin{bmatrix}b_n\end{bmatrix}_C&\end{bmatrix} \tag{5}
定理15中矩阵\underset{C \leftarrow \beta}{P}称为由\beta到C的坐标变换矩阵。乘以\underset{C \leftarrow \beta}{P}的运算将\beta –坐标变换为C-坐标,下图给出坐标变换方程(4)的说明
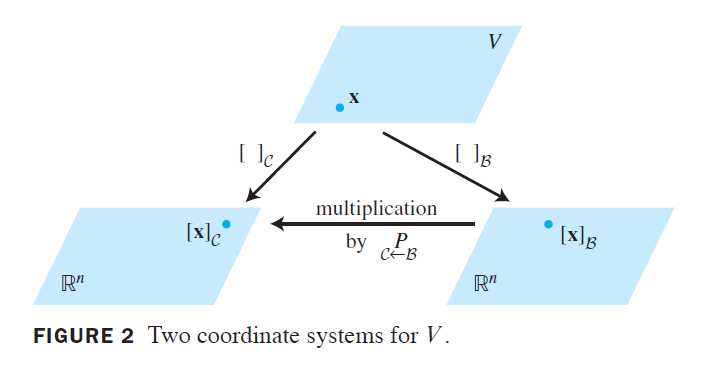
\underset{C \leftarrow \beta}{P}的列是线性无关的,这是因为它们是线性无关集\beta的坐标向量,于是得到\underset{C \leftarrow \beta}{P}是可逆的。将(4)量变左乘\left ( \underset{C \leftarrow \beta}{P} \right )^{-1},得
于是\left ( \underset{C \leftarrow \beta}{P} \right )^{-1}是将C-坐标变为\beta –坐标的矩阵,即
R^n中基的变换
若\beta=\{b_1,\dots,b_n\},\varepsilon是R^n中的标准基\{e_1,\dots,e_n\},则\begin{bmatrix}b_1\end{bmatrix}=b_1,\beta中其他向量也类似。在此情形下,\underset{\varepsilon \leftarrow \beta}{P}与4.4节中引入的坐标变换矩阵P_\beta相同,即
为了在R^n中两个非标准基之间变换坐标,我们需要定理15,定理15表明为解决基变换问题,我们需要原来的基关于新的基的坐标向量。
例2 设 b_1 =\left[\begin{array}{r} -9 \\ 1 \end{array}\right],b_2= \begin{bmatrix} -5 \\ -1 \end{bmatrix},c_1= \left[\begin{array}{r} 1 \\ -4 \end{array}\right],c_2= \left[\begin{array}{r} 3 \\ -5 \end{array}\right],考虑R^2中基\beta=\{b_1,b_2\},C=\{c_1,c_2\},求由\beta到C的坐标变换矩阵。
解 矩阵\underset{C \leftarrow \beta}{P}涉及b_1和b_2的C-坐标向量,设\begin{bmatrix}b_1\end{bmatrix}_c=\begin{bmatrix}x_1\\x_2\end{bmatrix},\begin{bmatrix}b_2\end{bmatrix}_c=\begin{bmatrix}y_1\\y_2\end{bmatrix},于是由定义
“`math
\begin{bmatrix}c_1&c_2\end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix}=b_1,
\begin{bmatrix}c_1&c_2\end{bmatrix} \begin{bmatrix} y_1 \\\ y_2 \end{bmatrix}=b_2,
“`
为了同步解出这两个方程组,将b_1和b_2扩大到系数矩阵中并简化之:
“`math
\left[\begin{array}{rr|rr}c_1&c_2&b_1&b_2\end{array}\right]=\left[\begin{array}{rr|rr}1&3&-9&-5\\
-4&-5&1&-1\\
\end{array}\right]
“`
“`math
\sim
\left[\begin{array}{rr|rr}1&0&6&4\\
0&1&-5&-3\\
\end{array}\right] \tag{7}
“`
于是\begin{bmatrix}b_1\end{bmatrix}_C= \left[\begin{array}{r}6 \\\ -5\end{array}\right],\begin{bmatrix}b_2\end{bmatrix}_C= \left[\begin{array}{r}4\\\ -3\end{array}\right],。因此所要求的坐标变换矩阵是
观察例2中的矩阵\underset{C \leftarrow \beta}{P},它已经出现在(7)中,这并不会令人感到意外,因为\underset{C \leftarrow \beta}{P}的第一列是行化简\left[\begin{array}{rr|rr}c_1&c_2&b_1&b_2\end{array}\right]\sim \left[\begin{array}{r|r}I&\underset{C \leftarrow \beta}{P}\end{array}\right]
求R^n中任意两个基之间的坐标变换矩阵具有类似的步骤。
