离散时间信号

离散时间信号的向量空间 $S$ 在4.1节中引入， $S$ 中一个信号是一个只定义在整数上的函数，同时可用一数列将其直观化，即 $\{y_k\}$ 。下图展示了三个典型的信号，它们的通项分别是 $(0.7)^k,1^k和(-1)^k$

信号空间S中的线性无关性

　为了简化符号，我们考虑一个仅包含三个信号 $\{u_k\}\{v_k\}\{w_k\}$ 的集合S，当方程

“`math
c_1u_k+c_2v_k+c_3w_k=0　对所有k成立 \tag{1}
“`
蕴含 $c_1=c_2=c_3=0时，\\{u_k\\},\\{v_K\\},\\{w_k\\}$ 恰好是线性无关的。这里说“对所有k成立”指对所有整数——正整数、负整数和0均成立。我们可能考虑从 $k=0$ 开始的信号，例如，这时“对所有k成立”将表示对所有 $k \ge 0$ 的整数成立。
　假设 $c_1,c_2,c_3$ 满足(1)式，那么方程(1)对任意三个相邻的值 $k,k+1和k+2$ 成立，这样(1)蕴含
“`math
\begin{align*}
c_1u_{k+1}+c_2v_{k+1}+c_3w_{k+1}=0　对所有k成立\\
c_1u_{k+2}+c_2v_{k+2}+c_3w_{k+2}=0　对所有k成立\\
\end{align*}
“`
从而 $c_1,c_2,c_3$ 满足

\left[\begin{array}{lll}u_k&v_k&w_k\\ u_{k+1}&v_{k+1}&w_{k+1}\\ u_{k+2}&v_{k+2}&w_{k+2}\\ \end{array}\right] \left[\begin{array}{l}c_1\\ c_2\\ c_3\\ \end{array}\right] = \left[\begin{array}{l}0\\ 0\\ 0\\ \end{array}\right]　对所有k成立　\tag{2}

这个方程组的系数矩阵成为信号的Casorati矩阵，这个矩阵的行列式成为 $\{u_K\},\{v_K\},\{w_K\}$ 的Casorati行列式。如果对至少一个 $k$ 值Casorati矩阵可逆，则(2)将蕴含 $c_1=c_2=c_3=0$ ,这就证明这三个信号是线性无关的。
　若Casorati矩阵不可逆，相应的信号通过检测可能线性相关也可能不是线性相关。但可以证明，如果这些信号是同一个齐次差分方程的所有解，则Casorati矩阵对所有k是可逆的且这些信号是线性无关的，否则Casorati矩阵对所有k都不可逆且这些信号是线性相关的。

线性差分方程

　给定数量 $a_0,\dots,a_n,a_0和a_n$ 不为零，给定一个信号 $z_k$ ,方程

“`math
a_0y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k=z_k　对所有k成立　\tag{3}
“`
称为一个**n阶线性差分方程(或线性递归关系)**。为了简化， $a_0$ 通常取为1，若 $\\{z_k\\}$ 是零序列，则方程是**齐次的**；否则，方程是**非齐次的**。

　例3　在数字信号处理中，像上面(3)那样的差分方程用来描述一个线性滤波器， $a_0,\dots,a_n$ 称为滤波器系数，若将 $\{y_k\}$ 看做输入， $\{z_k\}$ 看作输出，则对应齐次方程的解是过滤掉的信号，并被变换为零信号，让我们向如下滤波器输入两个不同的信号：

“`math
0.35y_{k+2}=0.5y_{k+1}+0.35y_k=z_k
“`
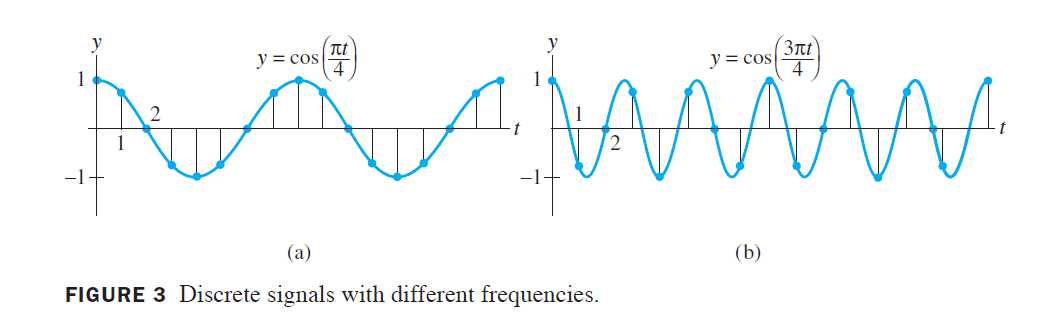
这里0.35是 $\sqrt{2}/4$ 的简写，第一个信号是由连续信号 $y=\cos(\pi t/4)$ 在整数值t抽样而生成，如下图所示。离散信号是 $\\{y_k\\}=\\{\dots,\cos(\pi /4),\cos(2\pi/4),\cos(3\pi/4),\dots\\}$ 。
为了简单，用 $\pm0.7$ 代替 $\pm \sqrt{2}/2$ ,从而
“`math
\{y_k\}=\{\dots,\underbrace{1}_{k=0},0.7,0,-0.7,-1,-0.7,0,0.7,1,0.7,0,\dots\}
“`
[![](http://www.wayln.com/wp-content/uploads/2021/05/wp_editor_md_2264a70b8b94d627b8bd874775f36702.jpg)](http://www.wayln.com/wp-content/uploads/2021/05/wp_editor_md_2264a70b8b94d627b8bd874775f36702.jpg)
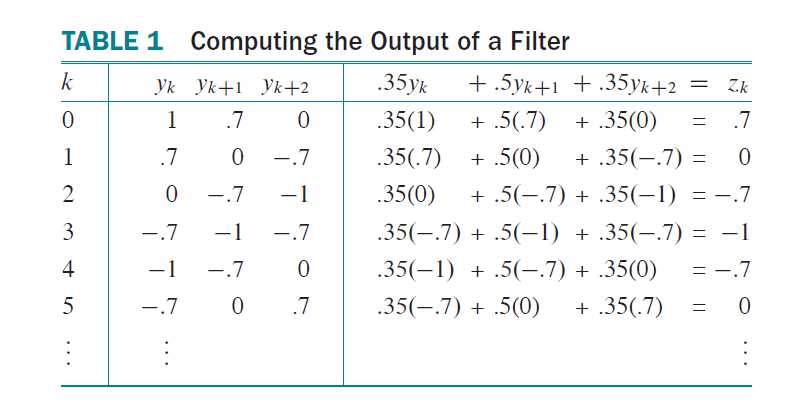
下表展示出输出序列 $\\{z_k\\}$ 的一个计算。这里0.35(0.7)是 $(\sqrt{2}/4)(\sqrt{2}/2)=0.25$ 的简写，将 $\\{z_k\\}$ 移动意向，输出就成为 $\\{y_k\\}$
[![](http://www.wayln.com/wp-content/uploads/2021/05/wp_editor_md_943b6171584943b13bd1588235dfcd45.jpg)](http://www.wayln.com/wp-content/uploads/2021/05/wp_editor_md_943b6171584943b13bd1588235dfcd45.jpg)
于是一个不同的输入信号由更高频率信号 $y=cos(3\pi t/4)$ 生成，见上图b。用与前面相同的抽样率去抽样，我们得到一个新的输入序列：
“`math
\{w_k\}=\{\dots,\underbrace{1}_{k=0},-0.7,0,0.7,-1,0.7,0,-0.7,1,-0.7,0,\dots \}
“`
当将 $\\{w_k\\}$ 输入给滤波器，则输出是零序列，若一个滤波器使 $\\{y_k\\}$ 能够通过，但将高频的 $\\{w_k\\}$ 截掉，则称该滤波器为**低通滤波器**。
　在许多应用中，序列 $\\{z_k\\}$ 由差分方程(3)的右端确定，满足(3)的一个 $\\{y_k\\}$ 成为这个方程组的一个解。

线性差分方程的解集

　给定 $a_1,\dots,a_n$ ，考虑映射 $T:S \rightarrow S$ ,将信号 $\{y_k\}$ 变换到信号 $\{w_k\}$ ，由下式给出

“`math
w_k=y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k
“`
容易验证T是一个线性变换，这蕴含其次方程
“`math
y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k=0　对所有k成立
“`
的解集是T的核（经T映射到零信号的信号的集合），进而这个解集是S的一个子空间，任何解的线性组合仍然是解。

定理16　若 $a_n \ne 0$ 且 $\{z_k\}$ 给定,只要 $y_0,\dots,y_{n-1}$ 给定，方程
$y_{k+n}+a_1y_{k+n-1}+ \dots+ a_{n-1}y_{k+1}+a_ny_k=z_k　对所有k成立　\tag{7}$
有唯一解。

定理17　n阶齐次线性差分方程
$y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k=0　对所有k成立\tag{10}$
的解集H是一个n维向量空间

非齐次方程

非齐次差分方程

y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k=z_k　对所有k成立\tag{11}

的通解能写成(11)的一个特解加上对应齐次差分方程(10)的一个基础解系的任意线性组合。

化简成一阶方程组

研究n阶齐次线性差分方程的现代方法是用等价的一阶差分方程组代替它，其中一阶差分方程写成如下形势：

x_{k+1}=Ax_k,　对所有k成立

这里向量 $x_k$ 在 $R^n$ 中， $A$ 是一个 $nxn$ 矩阵

一般而言，方程

y_{k+n}+a_1y_{k+n-1}+\dots+a_{n-1}y_{k+1}+a_ny_k=0,　对所有k成立

可重写成 $x_{k+1}=Ax_k$ ,对所有k成立，这里

x_k=\left[\begin{array}{l}y_k\\y_{k+1}\\\vdots\\y_{k+n-1}\end{array}\right]

A=\left[\begin{array}{ccccc}0&1&0&\dots&0\\ 0&0&1&&0\\ \vdots&&&\ddots&\vdots\\ 0&0&0&&1\\ -a_n&-a_{n-1}&-a_{n-2}&\dots&-a_1\\ \end{array}\right]

Filed under: 数学,线性代数,线性代数及其应用 - @ 2021年5月9日下午9:18

九霄之上