5.2 特征方程
行列式
设A是nxn矩阵,U是对A作行替换和行交换(不作行倍称)所得到的任一阶梯形矩阵,r是行交换次数,那么A的 行列式 \det A=(-1)^ru_{11}\dots u_{nn}。如果A可逆,那么u_{11},\dots,u_{nn}都是主元。否则,至少有u_{nn}为零,从而乘积u_{11}\dots u_{nn}为零。因此
\begin{cases}
(-1)^ru_{11}\dots u_{nn} {\text{当A可逆}}\\
0 {\text{当A不可逆}} \\
\end{cases} \tag{1}
定理(可逆矩阵定理(续))
设A是nxn矩阵,则A是可逆的当且仅当
s. 0不是A的特征值。
t. A的行列式不等于零。
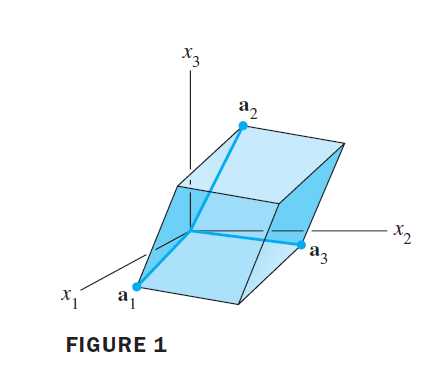
如果A是3×3矩阵,那么\left| \det A \right|是由A的列向量a_1,a_2,a_3生成的平行六面体的体积,见下图。平行六面体的体积不等于零当且仅当向量a_1,a_2,a_3线性无关,即矩阵A是可逆的。(如果向量非零且线性相关,他们位于同一个平面或一条直线上)
定理3 (行列式的性质)
设A和B是nxn矩阵
a. A可逆的充要条件是\det A \ne 0
b. \det AB=(\det A)(\det B)
c. \det A^T=\det A
d. 若A是三角形矩阵,那么\det A是A主对角线元素的乘积
e. 对A作行替换不改变其行列式值。做一次航交换使其行列式值符号改变一次。数乘一行后,行列式值等于用此数乘原来的行列式值。
特征方程
利用定理3(a),我们可以通过行列式来判断矩阵A-\lambda I是否可逆。数值方程\det (A-\lambda I)=0称为A的特征方程。
数\lambda是nxn矩阵A的特征值的充要条件是\lambda是特征方程\det (A-\lambda I)=0的根。
例3 求A=\left[ \begin{array}{rrrr}5&-2&6&-1\\0&3&-8&0\\0&0&5&4\\0&0&0&1\\ \end{array}\right]的特征方程
解 写出A-\lambda I并利用定理3(d):
0&3-\lambda&-8&0\\
0&0&5-\lambda&4\\
0&0&0&1-\lambda\\
\end{array}\right]
特征方程是
或
展开乘积,特征方程也可以写为
例1和例3的\det(A-\lambda I)是关于\lambda的多项式,可以看出,如果A是nxn矩阵,那么\det(A-\lambda I)是n次多项式,称为A的特征多项式
在例3中,由于因子(\lambda-5)在特征多项式中出现了2次,故称特征是5有重数2,。一般地,把特征值\lambda作为特征方程根的重数称为是\lambda的(代数)重数。
因为nxn矩阵的特征方程包含有一个n次多项式,如果算上重根,并允许有复根,则特征方程恰好有n个根。复根称为复特征值
#相似性
假如A和B是nxn矩阵,如果存在可逆矩阵P,使得P^{-1}AP=B,或等价地A=PBP^{-1},则称A相似于B。记Q=P^{-1},则有Q^{-1}BQ=A,即B也相似于A。故我们简单说A和B是相似的。把A变成P^{-1}AP的变换称为相似变换。
定理4 若nxn矩阵A和B是相似的,那么他们有相同的特征多项式,从而有相同的特征值(和重数)
警告
1. 矩阵\begin{bmatrix}2&1\\0&2\end{bmatrix}和>\begin{bmatrix}1&0\\0&2\end{bmatrix}即使有相同的特征值也不相似。
2. 相似性与行等价不是一回事(加入A行等价与B,则存在可逆矩阵E,使得1B=EA)对矩阵作行变换通常会改变矩阵的特征值
