5.4 特征向量与线性变换

Contents

1 线性变换的矩阵
2 V到V的线性变换
- 2.1 $R^n$上的线性变换
3 矩阵表示的相似性

在本节，我们将矩阵分解 $A=PDP^{-1}$ 理解为线性变换。我们还将看到变换 $x \mapsto Ax$ 实质上是简单的映射 $u \mapsto Du$ 。即使D不是对角矩阵时，对矩阵A和D仍有相似的解释。
在1.9节曾讲到，任意一个从 $R^n到R^m$ 的线性变换T可通过左乘矩阵A来实现，矩阵A成为T的标准矩阵。现在，我们对连个有限维向量空间之间的线性变换也做同样的描述。

线性变换的矩阵

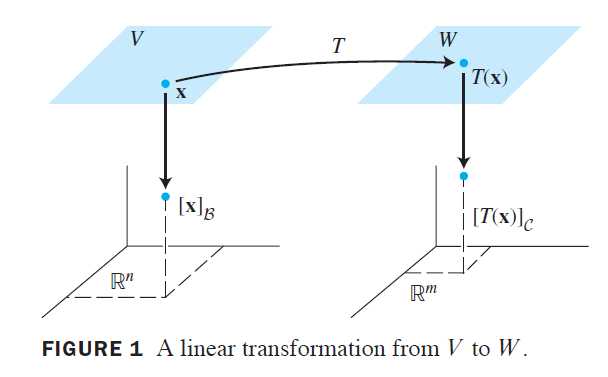
设V是n维向量空间，W是m维向量空间，T是V到W的线性变换，为了把T与矩阵相联系，我们指定 $\beta和C$ 分别是V和W的基。
若 $x \in V$ ,坐标向量 $\begin{bmatrix} x \end{bmatrix}_\beta \in R^n$ ，x的像 $T(x)$ 的坐标向量 $\begin{bmatrix} T(x) \end{bmatrix}_C \in R^m$ ，见下图，
容易找出 $\begin{bmatrix}x\end{bmatrix}_\beta$ 和 $\begin{bmatrix}T(x)\end{bmatrix}_C$ 之间的关系。设V的基 $\beta$ 是 $\{b_1,\dots,b_n\}$ 。若 $x=r_1b_1+\dots+r_nb_n$ ,则

\begin{bmatrix}x\end{bmatrix}_\beta=\begin{bmatrix}r_1\\ \vdots\\ r_n \end{bmatrix}

因为T是线性的，故

T(x)=T(r_1b_1+\dots+r_nb_n)=r_1T(b_1)+\dots+r_nT(b_n) \tag{1}

因为从W到 $R^m$ 的坐标映射是线性的（4.4节定理8），等式（1）可推出

\left[T(x)\right]_C=r_1\left[T(b_1)\right]_C+\dots+r_n\left[T(b_n)\right] \tag{2}

因为这些C-坐标向量都属于 $R^m$ ,向量等式（2）可以写为矩阵等式

\left[T(x)\right]_C=M\left[x\right]_\beta \tag{3}

其中

M=\begin{bmatrix}\left[T(b_1)\right]_C&\left[T(b)_2\right]_C&\dots &\left[T(b_n)\right]_C\end{bmatrix} \tag{4}

矩阵M是T的矩阵表示，称为T相对于基 $\beta$ 和C的矩阵，见下图

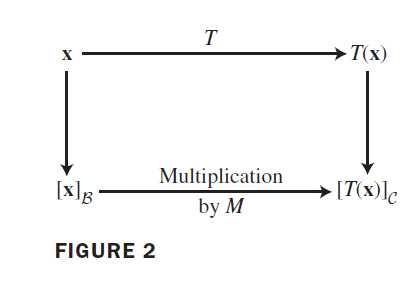
等式（3）表明，就坐标向量而言，T对x的作用相当于用矩阵M左乘x

V到V的线性变换

当W=V，C= $\beta$ 时，（4）中的M称为T相对于 $\beta$ 的矩阵，或简称为T的 $\beta-$ 矩阵，记为 $\left[T\right]_\beta$ ,见下图：

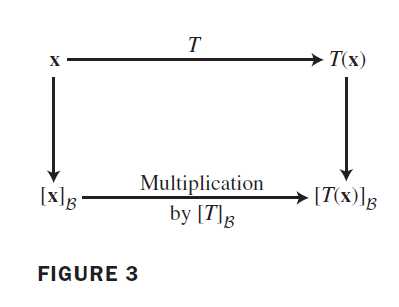
$V \rightarrow V$ 的线性变换T的 $\beta-$ 矩阵对所有V中的x,有

\left[T(x)\right]_\beta=\left[T\right]_\beta\left[x\right]_\beta \tag{5}

$R^n$上的线性变换

在涉及 $R^n$ 的应用问题中，线性变换首先表现为一个矩阵变换 $x \mapsto Ax$ 。假设A是可对角化的，那么存在由A的特征向量组成的 $R^n$ 的基。此时，下面的定理8表明T的 $\beta-$ 矩阵是对角矩阵，这样，把A对角化相当于找到变换 $x \mapsto Ax$ 的对角矩阵表示。

定理8（对角矩阵表示）
设 $A=PDP^{-1}$ ，其中D为nxn对角矩阵，若 $R^n$ 的基 $\beta$ 由P的列向量组成，那么D是变换 $x \mapsto Ax$ 的 $\beta-$ 矩阵

矩阵表示的相似性

定理8的证明没有用到D是对角矩阵这一事实。因此，若A相似于C，即由 $A=PCP^{-1}$ ,如果 $\beta$ 由P的列向量组成，则C是变换 $x \mapsto Ax$ 的 $\beta-$ 矩阵。分解 $A=PCP^{-1}$ 如下图所示：

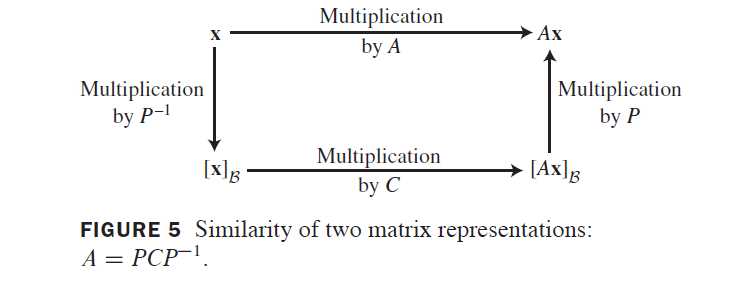
相反，若 $R^n \rightarrow R^n$ 的变换 $T:T(x)=Ax$ ,而 $\beta是R^n$ 的任意一个基，那么T的 $\beta-$ 矩阵相似于A

Filed under: 数学,线性代数,线性代数及其应用 - @ 2021年5月16日下午9:01